[ABC318E] Sandwiches 题解
[ABC318E] Sandwiches 题解
题意简述
给定包含 \(n\) 个整数的序列 \(a\),其中任意元素的值 \(a_i \in [1,n]\),统计包含三个元素的满足以下条件有序三元组数量:满足下标严格递增;满足第一个和最后一个元素相等,而中间的元素和两端的元素不相等。
记录三元组 \((a_i,a_j,a_k)\),即 \(1 \le i < j < k \le n , a_i = a_k \ne a_j\)。
思路分析
看到统计三元组就想到了扫描线。我们以 \(k\) 为扫描线,统计在 \(k\) 左侧的满足条件的三元组。
我们先观察到 \(a_i = a_k\) 是个比较严格的条件限制,于是我们可以 \(n\) 个 vector 维护每种数组的对应下标。现在我们画一张图:
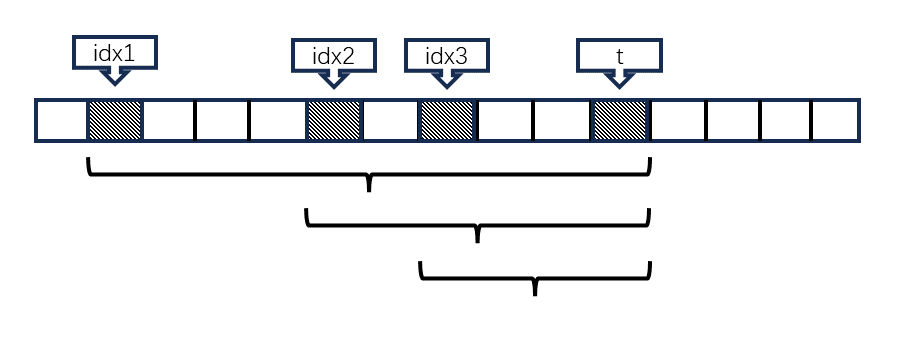
我们令当前扫描线位置为 \(t\),所有 和 \(a_t\) 数字相同的,在 \(t\) 左侧的元素,下标为 \({idx}_i\)。那么除了这些元素,剩下的元素数字一定和 \(a_t\) 不同。我们统计每对 \({idx}_i\) 到 \(t\) 之间(假设之前共有 \(m\) 个,\(i \in [1,m]\)),和 \(a_t\) 数字不同的元素个数,在加和即可。注意要减掉区间中间,包含的数字等于 \(a_t\) 的元素数量,当然这个可以通过 \(i\) 算出来。
我们可以发现:
\[{idx}_1\text{的贡献:} t - {idx_1} - 2 - 1 \\
{idx}_2\text{的贡献:} t - {idx_2} - 1 - 1 \\
{idx}_3\text{的贡献:} t - {idx_3} - 0 - 1 \\
\dots\\
{idx}_i\text{的贡献:} t - {idx_i} - (m-i) - 1 \\
\]
根据等差数列等相关知识,不难得出:
\[\]
\[\begin{aligned}
\text{总贡献} & = m \times t - \sum_i{{idx}_i} - m \times 1 - \frac{(m-1)m}{2} \\
& = m(t-1) - \frac{(m-1)m}{2} - \sum_i{{idx}_i}
\end{aligned}
\]
于是,我们甚至不用维护下标具体在哪里。我们只需要维护对于当前,之前下标的总和,和之前的下标总个数。计算完答案,在把当前的加入更新即可。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 5;
LL sumidx[N];
LL cntidx[N];
LL a[N];
LL n;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
}
LL ans = 0;
for(LL i = 1;i <= n;i++)
{
ans += cntidx[a[i]]*(i-1ll) - sumidx[a[i]] - (cntidx[a[i]]-1)*cntidx[a[i]]/2ll;
cntidx[a[i]]++;
sumidx[a[i]] += i;
}
cout << ans << "\n";
return 0;
}