【数学建模导论】Task01 数据处理与拟合模型
0 前言
感谢 DataWhale 的开源学习课程 intro-mathmodel,项目仓库在这。
现在开始,跟着Task01 进入数据类的学习,实现每一个代码,包括数据预处理、回归分析与分类分析、假设检验、随机过程与随机模拟、数据可视化图表、三种插值模型。
本篇是知识的梳理和总结,用以更好地食用教材,亦或作为后期复盘的资料。
学习重点在于各种常见的统计分析模型的区别总结。
1 数据与大数据
Drew Conway在2010年阐释“数据科学”的时候称:
“数据科学是统计学、计算机科学和领域知识的交叉学科”
2 数据的预处理
2.1 为什么需要数据预处理

在采集完数据后,
我们得到的原始数据往往非常混乱、不全面,模型往往无法从中有效识别并提取信息,
于是建模的首要步骤以及主要步骤便是数据预处理。
现在,我们先学习一个概念——稀疏。
对数据有一定的理解后再正式进行数据预处理操作。
2.2 使用 pandas 处理数据

重复数据:直接将其删除即可
缺失数据:主要是观察缺失率
- 缺失的数据项占比 较少(大概5%以内):这个时候如果问题允许可以把行删掉
- 缺失率稍微高一点(5%-20%)左右:就可以使用填充、插值的方法去处理
- 缺失率还高一些(20%-40%):就需要用预测方法例如机器学习去填充缺失数据了
- 如果一列数据有50%以上都是缺失的:可以把这一列都删掉(需要条件允许的情况下)
pandas dataframe的基础语法
# (1)Python创建一个数据框DataFrame:
import pandas as pd
import numpy as np
data = {'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat', 'snake', 'cat', 'dog', 'dog'],
'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df = pd.DataFrame(data)
df
#(2)显示该 DataFrame 及其数据相关的基本信息:
df.describe()
(3)返回DataFrame df 的前5列数据:
df.head(5)
#(4)从 DataFrame df 选择标签列为 animal 和 age 的列
df[['animal', 'age']]
#(5)在 [3, 4, 8] 行中,列为 ['animal', 'age'] 的数据
df.loc[[3, 4, 8], ['animal', 'age']]
#(6)选择列为visits中等于3的行 (: 在这里表示选取所有列。)
df.loc[df['visits']==3, :]
#(7)选择 age 为缺失值的行
df.loc[df['age'].isna(), :]
#(8)选择 animal 是cat且age 小于 3 的行
df.loc[(df['animal'] == 'cat') & (df['age'] < 3), :]
#(9)选择 age 在 2 到 4 之间的数据(包含边界值)
df.loc[(df['age']>=2)&(df['age']<=4), :] # 不能写联不等式,得拆开写
#(10)将 'f' 行的 age 改为 1.5
df.index = labels # 若要对DataFrame行索引操作,需要自行创建行索引。(DataFrame默认是没有激活行索引功能)
df.loc[['f'], ['age']] = 1.5
print(df)
#(11)对 visits 列的数据求和
df['visits'].sum()
#(12)计算每种 animal age 的平均值
df.groupby(['animal'])['age'].mean()
pandas处理数学建模中常见的任务
(数据去重、填补缺失值等等)
#(1)创建pandas dataframe
df = pd.DataFrame({'From_To': ['LoNDon_paris', 'MAdrid_miLAN', 'londON_StockhOlm',
'Budapest_PaRis', 'Brussels_londOn'],
'FlightNumber': [10045, np.nan, 10065, np.nan, 10085],
'RecentDelays': [[23, 47], [], [24, 43, 87], [13], [67, 32]],
'Airline': ['KLM(!)', '<Air France> (12)', '(British Airways. )',
'12. Air France', '"Swiss Air"']})
df
#(2)FlightNumber列中有某些缺失值,缺失值常用nan表示,请在该列中添加10055与10075填充该缺失值。
df['FlightNumber'] = df['FlightNumber'].interpolate().astype(int)
df
#(3)由于列From_To 代表从地点A到地点B,因此可以将这列拆分成两列,并赋予为列From与To。
temp = df['From_To'].str.split("_", expand=True) # expand=True 参数被设置时,意味着可以将这列拆分成两列
temp.columns = ['From', 'To']
#(4)将列From和To转化成只有首字母大写的形式。
temp['From'] = temp['From'].str.capitalize()
temp['To'] = temp['To'].str.capitalize()
#(5)将列From_To从df中去除,并把列From和To添加到df中
df.drop('From_To', axis=1, inplace=True)
df[['From', 'To']] = temp
df
#(6)清除列中的特殊字符,只留下航空公司的名字。
# str.extract 是一个用于从字符串中抽取匹配正则表达式的部分的方法。
# 这里的正则表达式 r'([a-zA-Z\s]+)' 匹配一个或多个字母 (a-z, A-Z) 或空白字符(\s)。+表示字母和空格的模式可以重复一次或多次。
# expand=False 参数被设置时,意味着返回的将是 Series,
# expand=True 参数为默认值,意味着返回的将是 DataFrame。
df['Airline'] = df['Airline'].str.extract(r'([a-zA-Z\s]+)', expand=False).str.strip()
df
#(7)在 RecentDelays 列中,值已作为列表输入到 DataFrame 中。
# 我们希望每个第一个值在它自己的列中,
# 每个第二个值在它自己的列中,
# 依此类推。如果没有第 N 个值,则该值应为 NaN。
# 将 Series 列表展开成名为 delays 的 DataFrame,
# 重命名列delay_1,delay_2等等,
# 并将不需要的 RecentDelays 列替换df为delays。
delays = df['RecentDelays'].apply(pd.Series)
delays.columns = ['delay_%s' % i for i in range(1, len(delays.columns)+1)]
df = df.drop('RecentDelays', axis=1).join(delays, how='left') # 左连接:确保其结果会包含左侧DataFrame(即df)的所有行
df
#(8)将delay_i列的控制nan都填为自身的平均值。
for i in range(1, 4):
df[f'delay_{i}'] = df[f'delay_{i}'].fillna(np.mean(df[f'delay_{i}'])) # f 是为了创建 格式化字符串字面量
df
#(9)在df中增加一行,值与FlightNumber=10085的行保持一致。
df = df._append(df.loc[df['FlightNumber'] == 10085, :], ignore_index=True)
df
#(10)对df进行去重,由于df添加了一行的值与FlightNumber=10085的行一样的行,因此去重时需要去掉。
df = df.drop_duplicates()
df
2.3 数据的规约
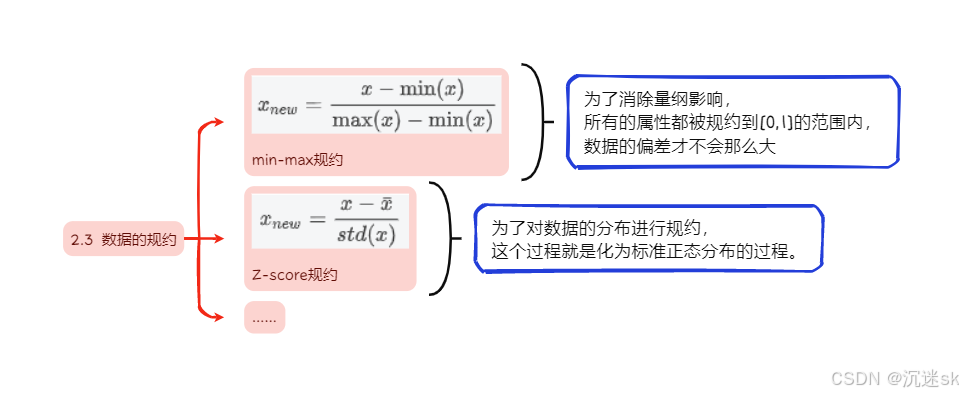
规约是为了形成对数据的更高效表示,学习到更好的模型。
它会保留数据的原始特征,但对极端值、异常值等会比较敏感。
3 常见的统计分析模型
3.1 回归分析与分类分析
回归分析与分类分析都是一种基于统计模型的统计分析方法。
它们都研究因变量(被解释变量)与自变量(解释变量)之间存在的潜在关系,
并通过统计模型的形式将这些潜在关系进行显式的表达。
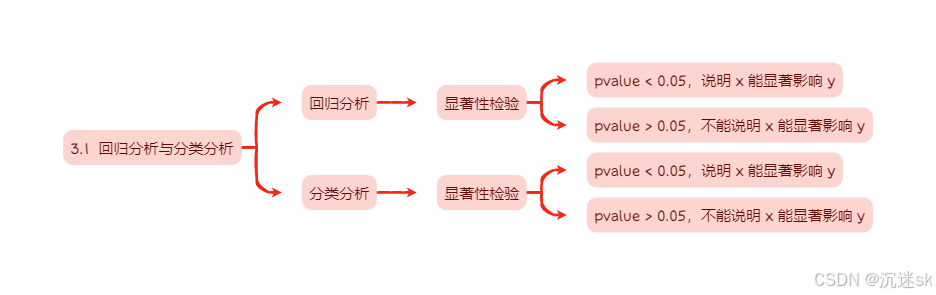
回归分析:其中因变量是连续变量,如工资、销售额;
使用 statsmodels.api 的 OLS 拟合、输出—— pvalue 数值来检验
- pvalue < 0.05,说明 x 能显著影响 y
- pvalue > 0.05,不能说明 x 能显著影响 y
分类分析:其中因变量是属性变量,如判断邮件“是or否”为垃圾邮件;
使用 statsmodels.api 的 formula.logit 拟合、输出—— pvalue 数值来检验
- pvalue < 0.05,说明 x 能显著影响 y
- pvalue > 0.05,不能说明 x 能显著影响 y
3.2 假设检验

对编程输出的 pVals 检验数值的解释:
pvalue < 0.05,拒绝原假设,
pvalue > 0.05,没有足够的证据拒绝原假设,
QQ图(可视化判断-正态分布概率图)
- 使用 scipy.stats 的 norm.rvs 随机生成服从正态分布的数据,
画 QQ 图,若数据接近红色直线,则初步判断数据服从正态分布。 - 使用 scipy.stats 的 chi2.rvs 随机生成服从卡方分布的数据,
画 QQ 图,若数据偏离红色直线,则初步判断数据不服从正态分布。
Shapiro-Wilk检验
尤其适用于小样本数据
- 使用 scipy.stats 的 shapiro 输出—— pVals 数值来检验
D'Agostino's K-squared检验(Omnibus检验)
- 使用 scipy.stats 的 normaltest 输出—— pVals 数值来检验
正态性数据检验-单样本t检验
- 使用 scipy.stats 的 ttest_1samp 输出—— pVals 数值来检验
非正态性数据检验-wilcoxon检验
- 使用 scipy.stats 的 wilcoxon 输出—— pVals 数值来检验
双独立样本的均值检验-正态性数据检验-双样本t检验
- 先使用 scipy.stats 的 levene 输出—— pVals 数值来检验
- 再使用 scipy.stats 的 ttest_ind 输出—— pVals 数值来检验
双独立样本的均值检验-非正态性数据检验-Mannwhitneyu秩和检验
是一种非参数检验
- 使用 scipy.stats 的 mannwhitneyu 输出—— pVals 数值来检验
这里的独立指的是抽样意义上的独立,
(即我们只需要保证这两个样本在选取的时候是“现实上”的互不影响就可以了)
而不是统计意义的独立,
(至于两者在数值上是否独立,通过独立性检验判断的独立性,我们并不关心)
教材说法:两个样本中,一个样本中的受试不能影响另一个样本中的受试。
不独立样本的均值检验(成对检验)-正态性数据检验-成对t检验
- 使用 scipy.stats 的 ttest_1samp 输出—— pVals 数值来检验
不独立样本的均值检验(成对检验)-非正态性数据检验-成对wilcoxon秩和检验
- 使用 scipy.stats 的 wilcoxon 输出—— pVals 数值来检验
不独立样本:这种情况多出现两个样本分别为同一个受试个体不同时间的受试结果
正态性数据检验-单因素方差分析(One-way ANOVA)
- 先使用 scipy.stats 的 levene 输出—— pVals 数值来检验
- 再使用 scipy.stats 的 f_oneway 输出—— pVals 数值来检验
非正态性数据检验-Kruskal-Wallis H 检验
是一种非参数检验
- 先使用 scipy.stats 的 levene 输出—— pVals 数值来检验
- 再使用 scipy.stats 的 mstats.kruskalwallis 输出—— pVals 数值来检验
3.3 随机过程与随机模拟
案例1:
为了改善道路的路面情况(道路经常维修,坑坑洼洼),
因此想统计一天中有多少车辆经过,因为每天的车辆数都是随机的
# 模拟仿真研究该道路口一天平均有多少车经过
import numpy as np
import simpy
class Road_Crossing:
def __init__(self, env):
self.road_crossing_container = simpy.Container(env, capacity = 1e8, init = 0)
def come_across(env, road_crossing, lmd):
while True:
body_time = np.random.exponential(1.0/(lmd/60)) # 经过指数分布的时间后,泊松过程记录数+1
yield env.timeout(body_time) # 经过body_time个时间
yield road_crossing.road_crossing_container.put(1)
hours = 24 # 一天24h
minutes = 60 # 一个小时60min
days = 3 # 模拟3天
lmd_ls = [30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40] # 每隔小时平均通过车辆数
car_sum = [] # 存储每一天的通过路口的车辆数之和
print('仿真开始:')
for day in range(days):
day_car_sum = 0 # 记录每天的通过车辆数之和
for hour, lmd in enumerate(lmd_ls):
env = simpy.Environment()
road_crossing = Road_Crossing(env)
come_across_process = env.process(come_across(env, road_crossing, lmd))
env.run(until = 60) # 每次仿真60min
if hour % 4 == 0:
print("第"+str(day+1)+"天,第"+str(hour+1)+"时的车辆数:", road_crossing.road_crossing_container.level)
day_car_sum += road_crossing.road_crossing_container.level
car_sum.append(day_car_sum)
print("每天通过交通路口的的车辆数之和为:", car_sum)
案例2:
现在,我们来仿真“每天的商店营业额”这个复合泊松过程吧。
首先,我们假设
每个小时进入商店的平均人数为:[10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10],
每位顾客的平均花费为:10元(大约一份早餐吧),
请问每天商店的营业额是多少?
# 模拟仿真研究该商店一天的营业额
import numpy as np
import simpy
class Store_Money:
def __init__(self, env):
self.store_money_container = simpy.Container(env, capacity = 1e8, init = 0)
def buy(env, store_money, lmd, avg_money):
while True:
body_time = np.random.exponential(1.0/(lmd/60)) # 经过指数分布的时间后,泊松过程记录数+1
yield env.timeout(body_time)
money = np.random.poisson(lam=avg_money)
yield store_money.store_money_container.put(money)
hours = 24 # 一天24h
minutes = 60 # 一个小时60min
days = 3 # 模拟3天
avg_money = 10
lmd_ls = [10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10] # 每个小时平均进入商店的人数
money_sum = [] # 存储每一天的商店营业额总和
print('仿真开始:')
for day in range(days):
day_money_sum = 0 # 记录每天的营业额之和
for hour, lmd in enumerate(lmd_ls):
env = simpy.Environment()
store_money = Store_Money(env)
store_money_process = env.process(buy(env, store_money, lmd, avg_money))
env.run(until = 60) # 每次仿真60min
if hour % 4 == 0:
print("第"+str(day+1)+"天,第"+str(hour+1)+"时的营业额:", store_money.store_money_container.level)
day_money_sum += store_money.store_money_container.level
money_sum.append(day_money_sum)
print("每天商店的的营业额之和为:", money_sum)
案例3:
艾滋病发展过程分为四个阶段(状态),
急性感染期(状态 1)、无症状期(状态 2), 艾滋病前期(状态 3), 典型艾滋病期(状态 4)。
艾滋病发展过程基本上是一个不可逆的过程,即:状态1 -> 状态2 -> 状态3 -> 状态4。现在收集某地600例艾滋病防控数据,得到以下表格

现在,我们希望计算若一个人此时是无症状期(状态2)在10次转移之后,这个人的各状态的概率是多少?
import numpy as np
# 研究无症状期病人在10期转移后的状态分布
def get_years_dist(p0, P, N):
P1 = P
for i in range(N):
P1 = np.matmul(P1, P)
return np.matmul(p0, P1)
p0 = np.array([0, 1, 0, 0])
P = np.array([
[10.0/80, 62.0/80, 5.0/80, 3.0/80],
[0, 140.0/290, 93.0/290, 57.0/290],
[0, 0, 180.0/220, 40.0/220],
[0, 0, 0, 1]
])
N = 10
print(str(N)+"期转移后,状态分布为:", np.round(get_years_dist(p0, P, N), 4))
4 数据可视化
4.1 Python 三大数据可视化工具库的简介

Matplotlib 的绘图逻辑是:一句话一个特征。
Seaborn 把数据拟合等统计属性高度集成在绘图函数中,绘图功能还是构筑在Matplotlib之上。
Plotnine 的绘图逻辑是:一句话一个图层。
4.2 基本图表 Quick Start
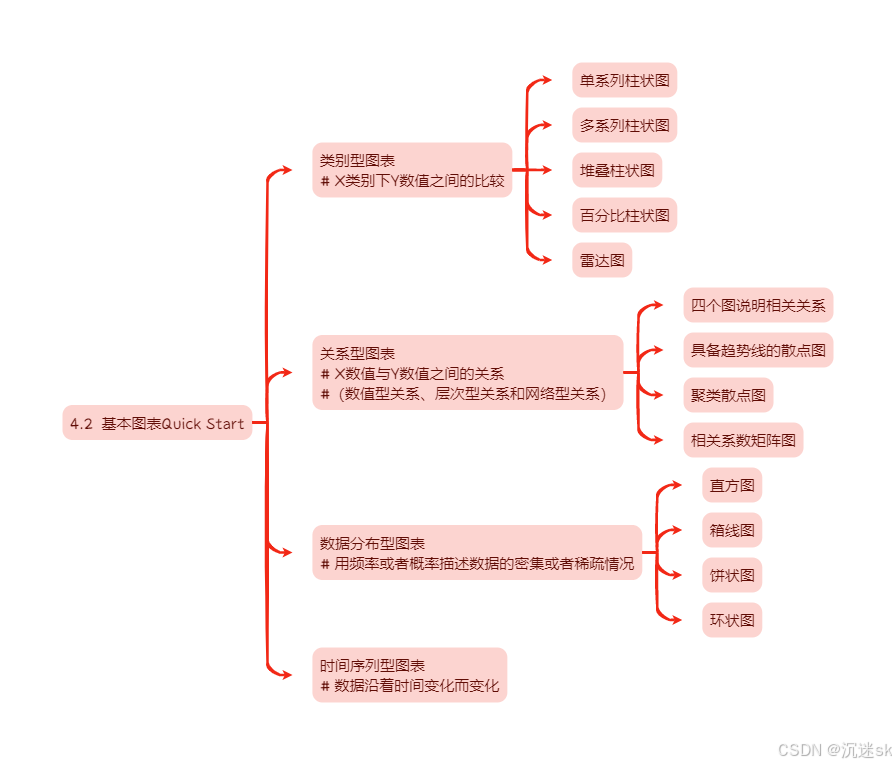
5 插值模型
5.1 线性插值法
$$
{L_1}(x) = {y_k} + \frac{{{y_{k + 1}} - {y_k}}}{{{x_{k + 1}} - {x_k}}}(x - {x_k}) \tag{5.1}
$$
5.2 三次样条插值
$$
{a_i}x_i^3 + {b_i}x_i^2 + {c_i}{x_i} + {d_i} = {a_{i + 1}}x_{i + 1}^3 + {b_{i + 1}}x_{i + 1}^2 + {c_{i + 1}}{x_{i + 1}} + {d_{i + 1}} \tag{5.2}
$$$$
3{a_i}x_i^2 + 2{b_i}{x_i} + {c_i} = 3{a_{i + 1}}x_{i + 1}^2 + 2{b_{i + 1}}{x_{i + 1}} + {c_{i + 1}} \tag{5.3}
$$$$
6{a_i}{x_i} + 2{b_i} = 6{a_{i + 1}}{x_{i + 1}} + 2{b_{i + 1}} \tag{5.4}
$$
5.3 拉格朗日插值
对于一组数据{y}和下标{x},定义n个拉格朗日插值基函数:
$$
{l_k}(x) = \prod\limits_{i = 0,i \ne k}^n {\frac{{x - {x_i}}}{{{x_k} - {x_i}}}} \tag{5.5}
$$
这本质上是一个分式,当 x=xk 时 lk(x)=1,这一操作实现了离散数据的连续化。
按照对应下标的函数值加权求和可以得到整体的拉格朗日插值函数:
$$
L(x) = \sum\limits_{k = 0}^n {{y_k}{l_k}(x)} \tag{5.6}
$$
Read more
- 数学建模导论 intro-mathmodel
(知识密度大、代码理论兼备)
https://datawhalechina.github.io/intro-mathmodel/#/ - Python科学计算 scientific-computing(数学建模导论的前置课程)
(知识密度小、代码实操强悍)
https://datawhalechina.github.io/scientific-computing/#/ - 数据总动员 Data-Story
(统计分析的原理&大量数学知识)
https://github.com/Git-Model/Modeling-Universe/tree/main/Data-Story